SAMSA Workshop
Workshop on Series, Automata, Matrices, Symbolic dynamics, and their Applications
Aim:
The aim of SAMSA is to bring together researchers working on weighted automata, matrix reachability, noncommutative power series and symbolic dynamics in order to identify common open problems and ways to attack them by techniques across the mentioned areas. The plan is to discuss recent results, emerging research directions, promising applications, open problems and stimulate cooperation among researchers working in these fields.
Topics:
Topics of interest include (but are not limited to):
- weighted automata,
- matrix reachability,
- semigroups,
- noncommutative power series,
- symbolic dynamics,
- linear recurrence sequences.
Program
The programme will consists of invited talks and tutorials, and short contributed talks from participants. The full schedule is posted below, the order of contributed talks will be published shortly.
Schedule
Click the underlined session to see jump to the speaker(s) of that session.
Participants are invited to go to lunch in the local area in small groups. There are many options within a short walk of the venue including a modern food court at the nearby Elektrownia Powiśle.
Picnic Dinner
On Wednesday evening, from 17:30 we will have a (bring your own food and drink) picnic in North Eastern corner of Pole Mokotowskie adjacent to the Politechnika metro stop.
For the exact location see: Google Maps or what3words///examine.lively.travel.
Invited Speakers:
Monday
Abstract (Click to expand)
I'll present Path-Complete control, a meta-optimization technique aiming at designing efficient optimization programs, initially introduced for stability analysis of switched linear systems, but later generalized to other control problems. These optimization programs are conveniently represented by an automaton. I'll review the seminal characterization results, which establish equivalence between universal automata and valid stability certificates. I'll provide a Lyapunov-theoretic interpretation of these stability criteria thanks to automata-theoretic tools. I will introduce the comparison problem, namely to characterize the partial order between path-complete criteria, in terms of their conservativeness. We will see that this partial order actually depends on the used template of Lyapunov functions, making another interesting connection between algebraic geometry and combinatorics. If time allows I will comment on generalization of the technique to other problems/systems in Control Engineering.Abstract (Click to expand)
I will introduce several open problems on Path-Complete Lyapunov Functions: from elementary ones to more open, prospective ones. They all blend symbolic dynamics, automata theory, algebraic geometry and (linear) dynamical systems theory.
For example, for practical purpose, it is crucial to understand when a particular Path-Complete Criterion is less conservative than another one. I'll focus on this problem, which is essentially an algebraic geometry problem. I will mention recent advances, which take into account the used template of candidate Lyapunov functions. We solved the comparison problem for several templates, making use of tools from automata theory (simulation,...), graph theory (Hall's marriage theorem), and convex geometry (duality,...). The general problem remains open, and I will comment on future directions.
I'll also raise the question of the existence of a canonical form for Path-Complete criteria, and present a statistical version of the comparison problem mentioned above, which seems highly relevant in practice, but for which very little is understood for the moment.
Tuesday

Abstract (Click to expand)
We present recent results on shuffle-finite power series in noncommuting variables, a nonlinear generalisation of Schutzenberger's rational series motivated by enumerative combinatorics, concurrency theory, and control theory. In the first part of the presentation, we show that the zeroness problem is decidable for this class, by presenting a natural algorithm based on polynomial ideals and Hilbert's finite basis theorem. We then show that other natural problems such as equality and commutativity are also decidable, by reduction to zeroness.
In the second part of the presentation, we apply shuffle-finite series to nonlinear control theory. This is based on Fliess' 1970's work showing that continuous-time deterministic input-affine state-polynomial control systems are uniquely described by their characteristic power series in noncommuting variables. As a consequence, one can decide equivalence for such systems by reducing to the equality problem for the corresponding characteristic power series. Other problems relevant to control theory can be tackled by the same approach: input independence, input linearity, and input analiticity.
The connection with the first part of the presentation lies in the observation that the class of characteristic series of input-affine state-polynomial control systems is exactly the class of shuffle-finite series. Consequently, we can decide equivalence and the other problems by reduction to corresponding problems on shuffle-finite series, obtaining novel results in the formal verification of control systems. It is open whether one can extend these results to the general class of polynomial control systems.
Abstract (Click to expand)
For a given system of polynomial ODEs and a given initial condition x(0) from Q^k there is exactly one tuple of power series x from Q[[t]]^k satisfying the ODEs whose constant term equals the initial condition. The invariant ideal Inv is the set of all polynomials p vanishing on this tuple of power series p(x) = 0. Thanks to the Hilbert finite basis theorem, Inv is finitely generated as an ideal. The open problem is to compute a finite basis for Inv. It amounts to understanding all possible algebraic relations between the components of x and its computability would be a deep insight inside the algebraic structure of ODEs.
Here are three special cases, for which the problem is solved. The first special case is the zeroness problem, which can be restated as the membership problem for Inv. The second special case is about linear ODEs (i.e., continuous-time linear dynamical systems), for which Inv is computable as a consequence of results of Derksen, Jeandel, and Koiran from 2005. Finally, the third special case says that for every degree bound D, one can compute all invariants of degree <= D.
We also compare this problem to the discrete-time setting, where bases are uncomputable for polynomial automata (Hrushovski, Ouaknine, Pouly, and Worrell JACM'23) and Skolem-hard for polynomial recursive sequences (Müllner, Moosbrygger, Kovacs POPL'24).
Wednesday and Thursday
Abstract (Click to expand)
We study density of rational languages under shift invariant probability measures on spaces of two-sided infinite words, which generalizes the classical notion of density studied in formal languages and automata theory. The density for a language is defined as the limit in average (if it exists) of the probability that a word of a given length belongs to the language. We establish the existence of densities for all rational languages under all shift invariant measures. We also give explicit formulas under certain conditions, in particular when the language is aperiodic or when it is a group language. Our approach combines tools and ideas from semigroup theory and ergodic theory.We list a number of open problems (joint work with Valérie Berthé, Herman Goulet-Ouellet, Carl-Fredrik Nyberg-Brodda and Karl Petersen)
Abstract (Click to expand)
We develop on examples the techniques of computation for the density of a rational language: computation of the J-class of an irreducible shift in a finite monoid, computation of the substitutions making a minimal skew product a morphic shift, computation of the invariant measure on a primitive substitution shift,...Thursday
 Photo from here
Photo from here
Abstract (Click to expand)
This talk will be a general survey of what can we decide about iterations of linear maps. Given a point x in euclidean space and a matrix A, we will ask which properties of the sequence Anx are decidable. Equivalently, what can we formally verify for a class of programs made out of a single loop inside which only linear updates are allowed. I will begin by translating problems about weighted automata, Markov chains, and linear recurrence sequences, into questions about the sequence Anx, and then continue with describing the principal techniques, focusing on open questions and where the difficulties lie.Abstract (Click to expand)
This tutorial will be about a single problem: given algebraic sets S, T, and a linear map A, does there exist a point in S whose orbit under A reaches T. One can ask more precisely: (1) reaches at least 1 time, (2) at least 10 times, (3) infinitely many times, (4) with positive frequency (e.g. 20% of the time the trajectory is in T). We do not yet know whether there exists a procedure for Problem (1). Problem (2) is undecidable. Problem (3) is known to be decidable for diagonalisable maps, and Problem (4) is decidable. I will explain the core ideas and techniques behind these results.Friday
 Photo from here
Photo from here
Abstract (Click to expand)
We will survey some recent results concerning decision problems for probabilistic and quantum automata. Our aim will be to map the boundary between tractable problems, for which an efficient decision procedure is known, and those which are intractable, via reductions of NP-hard, PSPACE-hard, or undecidable problems. We will see a number of proof strategies, drawing on ideas from linear algebra, branches of number theory, complexity theory, and graph theory, and identify avenues for future research directions.Abstract (Click to expand)
We will see details of how to prove the undecidability of the injectivity problem for quantum automata using a reduction from the mixed Post’s correspondence problem from formal language theory. This will be done in two ways; firstly via a direct encoding and using free rotation groups and secondly via an encoding using rational polynomial packing functions, which removes the need to have a non-rational real algebraic initial state vector of the automata.Participant talks:
We encouraged contributed talks which do not fit in the format of more formal conferences, such as reports on failed attempts, presentations of old results that did not receive enough attention, open-ended potential research directions, unexpected connections between different areas, open problems and possible lines of attack.
Matrix semigroups and finite automata
Monday 15:30Wojciech Czerwiński (University of Warsaw, Poland)
The path equivalence problem and Laurent polynomials
Abstract: I will talk about our failed attempt to solve the path equivalence problem (given two systems, do they have the same number of accepting paths for each input word) for any nontrivial extension of finite automata. Although we did not obtain any algorithm we found interesting connections with Laurent polynomials and some mysterious connections with functional analysis, I will show you that.
I believe that this direction of research is an important and fundamental one and should be pursued, but at the moment I have no clue how to attack it.
Reino Niskanen (Liverpool John Moores University, UK)
A different way of simulating Turing machines with matrices [Slides]
Abstract: It is well-known that a lot of algorithmic problems for matrix semigroups are undecidable. For example, when given a finitely generated matrix semigroup $S=\{M_1,\ldots,M_k\}$ and a matrix M one could ask whether the given matrix belongs to the generated semigroup, i.e., whether $M\in\langle S\rangle$ holds or not? The undecidability results in the literature tend to utilise embeddings from $\{a,b\}^*\times\{a,b\}^*$ into the desired matrix semigroup whilst ensuring that the structural constraints of the semigroup are preserved. In this talk, I will give a brief overview of some existence and non-existence results for embeddings and show how a non-standard embedding can lead to an undecidability result where a Turing machine is simulated using matrices.
Alexander Guterman (Bar-Ilan University, Israel)
Combinatorial indices for matrix semigroups and finite automata [Slides]
Abstract: There is a number of important combinatorial matrix classes such as indecomposable matrices, primitive matrices, scrambling matrices, chainable matrices, etc., that are useful both in fundamental investigations and in applications. The central approach to study these classes is via certain their numerical invariants. To list a few of them, we mention matrix exponent, scrambling index and solidarity index.
In the talk we give a short exposition of these notions and their applications to the theory of non-negative matrix semigroups and theory of finite automata.
We illustrate the importance of this approach by presenting several recent results related to the extensions of classical results due to Perron, Frobenius and Wielandt to matrix semigroups. This is a joint work with Yu.A. Alpin, A.M. Maksaev, E.R. Shafeev.
Weighted automata and power series
Tuesday 11:00Gorav Jindal (University of Warsaw, Poland)
Rationality of Formal Power Series over Subsemirings [Slides]
Abstract: For an alphabet $\Sigma$, a formal power series over a semiring $R$ is a function $f: \Sigma^* \to R$. Weighted automata over $R$ are used to recognize such series. The well-known Fliess' theorem states that when $R$ is a field, the minimal automaton recognizing $f$ has a size equal to the rank of its associated Hankel matrix $H_f$. Given a weighted automaton over $R$ recognizing a formal power series $f$, and a subsemiring $S$ of $R$, we investigate the question of whether $f$ is also rational over $S$. This means determining if there exists a weighted automaton with entries in $S$ that also recognizes $f$, under the promise that the image of $f$ is contained within $S$, i.e., $f(\Sigma^*) \subseteq S$.
In this talk, we primarily consider the cases when $R = \mathbb{R}$ is the real field and $S = \mathbb{R}_{\geq 0}$ is the set of non-negative reals. We discuss the challenges and adaptations involved in relating the size of weighted automata over $\mathbb{R}_{\geq 0}$ to specific factorizations of the Hankel matrix, such as non-negative and residual factorizations. We will discuss some failed attempts to solve this problem and some open questions.
Yahia Idriss Benalioua (Aix-Marseille University, France)
On the complexity of computing the linear hull of weighted automata over $\mathbb{Q}$ [Slides]
Abstract: The linear hull (LH) of a weighted automaton (WA) is an invariant, recently introduced by [Bell & Smertnig, 2021], that allows to decide the unambiguity or sequentiality of WA over a field. We showed in [Benalioua, Lhote & Reynier, 2024] that the LH of a WA can be used to solve the register minimization problem for cost register automata (CRA) and gave a 2EXPTIME procedure for its computation. However, the question of the tightness of this complexity bound remains open.
In this talk, I will present the idea underlying this procedure, how it relates to minimization problems for CRA and I will show how its complexity is linked to bounding the number of irreducible components of the linear Zariski closure of a finitely generated group of matrices.
If time permits, I will also mention how those results generalize to weighted tree automata and the challenges faced in this setting.
Arka Ghosh (University of Bordeaux, France)
Residual weighted finite automata
Abstract: A weighted finite automata (WFA) is called residual if the cone generated by the rows of its Hankel matrix is finitely generated. Residual WFAs are better behaved than WFAs in general. For example, they admit unique conical basis as a consequence of which they are learnable. They are closed under reversal, as a consequence of which non-negativity of residual WFAs is decidable. The questions we are interested in are whether residuality is a decidable property, and whether positivity of residual automata can be decided.
Register automata and verification
Tuesday 15:30Łukasz Kamiński (University of Warsaw, Poland)
Semilinear and rational sets with data [Slides]
Abstract: The family of semilinear sets admits several equivalent characterisations: sets definable in Presburger arithmetic, rational subsets of the monoid (N^d, +), Parikh images of regular languages. This notion can be generalised to data vectors, where coordinates are indexed by an orbit-finite set. However, in this extended setting, the classical equivalences break down. For instance, semilinear sets of data vectors form a strict subset of the family of rational sets of data vectors. The latter are conjectured to coincide with the Parikh images of languages recognised by register automata. These families remain poorly understood and continue to offer a rich source of open problems.
Jingjie Yang (University of Oxford, UK)
Orbit-finite-dimensional vector spaces [Slides]
Abstract: Whilst N^2 is an infinite set, under bijective renamings it only consists of two orbits: the pairs with distinct entries, and those with the same entry repeated twice. As such N^2 is an orbit-finite set; in turn, the vector space with basis N^2 can be called orbit-finite-dimensional. I will show such spaces have finite length, so language equivalence for weighted register automata is decidable over many infinite alphabets. This extends the work of Bojańczyk, Fijalkow, Klin, and Moerman [LICS’21/TheoretiCS’24].
Antonio Casares (University of Warsaw, Poland)
Safety and liveness. What are these things? [Slides]
Abstract: In this talk, I will define safe and live languages and present safety-liveness decompositions. The content of this talk is mostly folklore, but it might also include results from:
- B. Alpern, F.B. Schneider: Defining liveness, Inf. Process. Lett., 1985
- T. Henzinger, N. Mazzocchi and N.E. Saraç: Quantitative Safety and Liveness, FoSSaCS, 2023
Vector addition systems and timed automata
Wednesday 11:00Łukasz Orlikowski (University of Warsaw, Poland)
Low-Dimensional VASS: Where Our Tools Fail Us [Slides]
Abstract: The complexity of the reachability problem in Vector Addition Systems with States (VASSs) remained an open question for several decades. Although the problem was eventually shown to be Ackermann-complete, many fundamental questions about VASSs are still unresolved. In fact, even the reachability problem itself is not yet fully understood. A key indication of this is the presence of significant complexity gaps for low-dimensional cases.
In this talk, I will briefly outline the current state of the art regarding the reachability problem in low-dimensional VASSs and discuss possible future research directions. The main focus will be on identifying where existing techniques fall short and why current complexity bounds remain unimproved.
Clotilde Biziere University of Bordeaux, France)
A Forward Construction of Inductive Invariants for Vector Addition Systems [Slides]
Abstract: The first and best-known algorithm for the reachability problem in Vector Addition Systems (VAS) is a decomposition developed by Mayr in 1981, later simplified by Kosaraju and Lambert. In 2011, Leroux introduced a completely different approach. He showed that non-reachability can be certified by semilinear inductive invariants: if a target configuration is unreachable from the initial one, then there exists a semilinear set containing the initial configuration, closed under the VAS transitions, and excluding the target. As a consequence, VAS reachability can be decided by two semi-algorithms: one that enumerates runs, and one that searches through semilinear sets for such invariants.
Leroux’s construction of inductive invariants proceeds by alternately expanding two semilinear sets, which we refer to as the Source and the Trap, ensuring that no configuration in the Source can reach any configuration in the Trap. These sets are initially the singleton sets containing the initial and target configurations, respectively. To expand the Trap, one overapproximates the forward reachability set of the Source by a semilinear set, and adds its complement to the Trap. Symmetrically, the Source is expanded by adding the complement of a semilinear overapproximation of the Trap's backward reachability set. Once the Source and Trap become complements of each other, the Source is an inductive invariant.
This symmetric construction offers little insight into the structure of the resulting invariant. For instance, it does not guarantee that the invariant is periodic when the VAS itself is periodic. Moreover, the approach does not seem to generalize to Branching VAS, an asymetric extension of VAS where transitions may have multiple source configurations.
In this talk, I present a new, purely forward construction of inductive invariants for VAS, developed with Jérôme Leroux and Grégoire Sutre. We believe this construction constitutes a step toward decidability of reachability in Branching VAS.
Andrew Scoones (University Paris-Est - Créteil, France)
Reachability for Multi-Priced Timed Automata and Diophantine Approximation [Slides]
Abstract: Timed automata are a widely studied model of real-time systems that extend classical finite state-automata with real-valued variables, called clocks, that evolve with derivative one and which can be queried and reset along transitions. Multi-Priced Timed Automata (MPTA) further extend timed automata with write-only variables, called observers, that have a non-negative slope that can change from one location to another. We consider the domination problem: given an MPTA and a target t, is there a run on the automata such that the value of the run is less than t pointwise? This is known to be undecidable if negative rates are allowed.
We introduce a variant of this problem by introducing a slack parameter. This allows us to transfer the problem to a Diophantine problem. While we show that this problem is still undecidable, we show decidability in the bounded case, through methods from Diophantine approximation and the geometry of numbers. In this talk, I will focus on Diophantine Approximation methods that are not in the paper, but may be able to be translated back into results on MPTA.
Recurrence sequences and loop invariants
Thursday 15:30George Kenison (Liverpool John Moores University, UK)
The Membership Problem for Hypergeometric Sequences [Slides]
Abstract: Take as inputs a rational-valued recurrence sequence and a rational target, the Membership Problem asks to procedurally determine whether the specified target is a term in the input sequence. In this talk we will restrict our attention to hypergeometric sequences (the class of sequences that obey a first-order linear recurrence relation with polynomial coefficients). In this talk, we will discuss both the difficulty with settling decidability and survey results in this setting. Time permitting, we will outline the approaches in recent works as well as directions for future work.
Results surveyed in this talk are taken from collaborations with J. Konieczny, F. Luca, K. Nosan, A. Scoones, M. Shirmohammadi, and J. Worrell.
Piotr Bacik (University of Oxford, UK and Max Planck Institute for Software Systems, Saarland University, Germany)
On the complexity of the Skolem Problem
Abstract: The Skolem Problem asks whether a given linear recurrence sequence has a zero term. Decidability of this problem has famously been open for over 90 years. Special cases are known - in particular for sequences of order at most 4. By following the proof it is easy to determine that the complexity of the Skolem Problem for such sequences is in NP^{RP}. To date, this is the best known complexity upper bound.
In the talk I will discuss a soon-to-be submitted result showing the Skolem Problem at order 4 is in coRP, and directions for improvements.
Anton Varonka (TU Wien, Austria)
Invariants without a loop
Abstract: Guided by the question “What polynomial invariants can loops with linear updates have?”, we are desperately searching for methods of proving that certain d-variate polynomials cannot be loop invariants of any non-trivial linear loop with d variables. A linear loop is described by (A, x) where A is a square matrix of size d and x is a vector of size d, both having rational entries. A polynomial invariant P is a polynomial in d variables such that P vanishes on each A^nx.
Randomness and communication
Friday 11:00Qiyi Tang (University of Liverpool, UK)
Trace Inequivalence for MDPs is in P
[Slides]
Abstract: We study the algorithmic comparison of two labelled MDPs whether there exist strategies such that the MDPs become (in)equivalent in terms of trace equivalence. We provide the first polynomial-time algorithms for computing strategies to make the two labelled MDPs inequivalent if such strategies exist. This is joint work with Stefan Kiefer.
Mikołaj Bojańczyk (University of Warsaw, Poland)
Two-party computation for functions with string inputs [Slides]
Abstract: I will describe a model of computation, which describes functions that input strings, and output elements from some domain, such as the Booleans, or strings, or a field. The idea is that there are two parties, Alice and Bob, who cooperate to compute the output of the function. For a given input string, an adversary chooses a partition w=w1w2, and sends the words w1 and w2 to Alice and Bob, respectively. Alice and Bob then exchange a constant number of messages, using some operations in the output domain, in a way that results in the output of the function. We will show that for various output domains, the model coincides with standard notions. In particular, for Boolean outputs, it gives regular languages, and for outputs in a field, it gives weighted automata. Joint work with Aliaume Lopez, Rafał Stefański, and Omid Yaghoubi.
Organisation
SAMSA Workshop: Series, Automata, Matrices, Symbolic dynamics, and their Applications is organised by:
Contact:
Click to email all three organisers.Location:
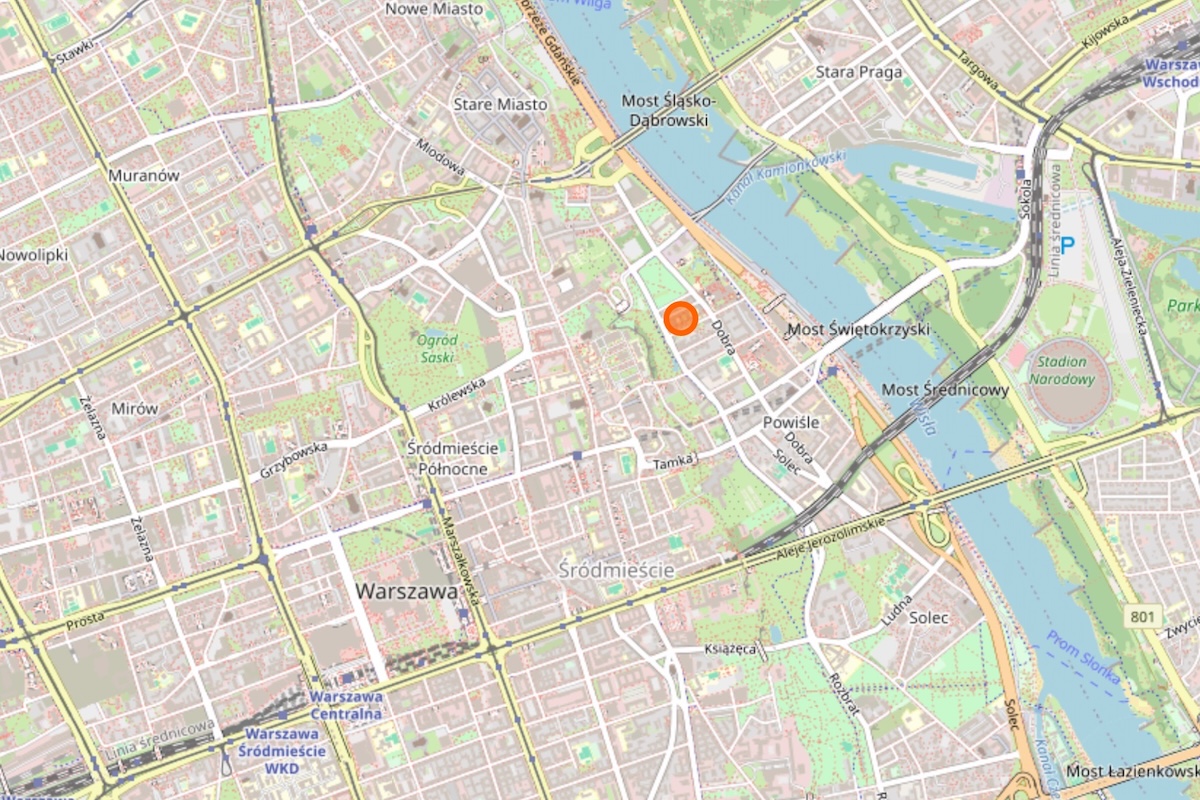
The SAMSA workshop takes place in person at the Faculties of Modern Languages (Wydział Neofilologii).
Address: 55 Dobra street at the University of Warsaw, Poland. (The closest entrance to the room is on Browarna.)
Most sessions will take place in Room 1.110 (first floor, zero indexed). Sessions on Tuesday afternoon will take place in the adjacent Room 1.120.
Attending:
If you are interested in attending in the Workshop, please contact the organisers (please include all three).
Financial support:
Supported by IDUB Thematic Research Programmes (POB III), Faculty of Mathematics, Informatics and Mechanics, University of Warsaw.